私たちの研究室では，制御工学・制御理論を基盤として，合成生物学，分子ロボティクスや機械学習などの分野にまたがる学際的な研究を行っています．

制御工学 × 生体分子システム

合成生物学やDNAナノテクノロジーの発展により，近年，DNAやタンパク質などの分子を素材として，細胞で生じるような反応システムを人工的に構築することが可能になりつつあります． このような人工生体分子システムにより，生体分子ネットワークの動作原理を理解するだけでなく，化学の原理で動作する新たな情報処理デバイスや分子機械・分子ロボットの実現が期待されています． このような応用を進めるためには，微生物や分子レベルの生化学反応を「理解し予測する」だけでなく，「設計し制御する」ことがますます重要になると考えられます．

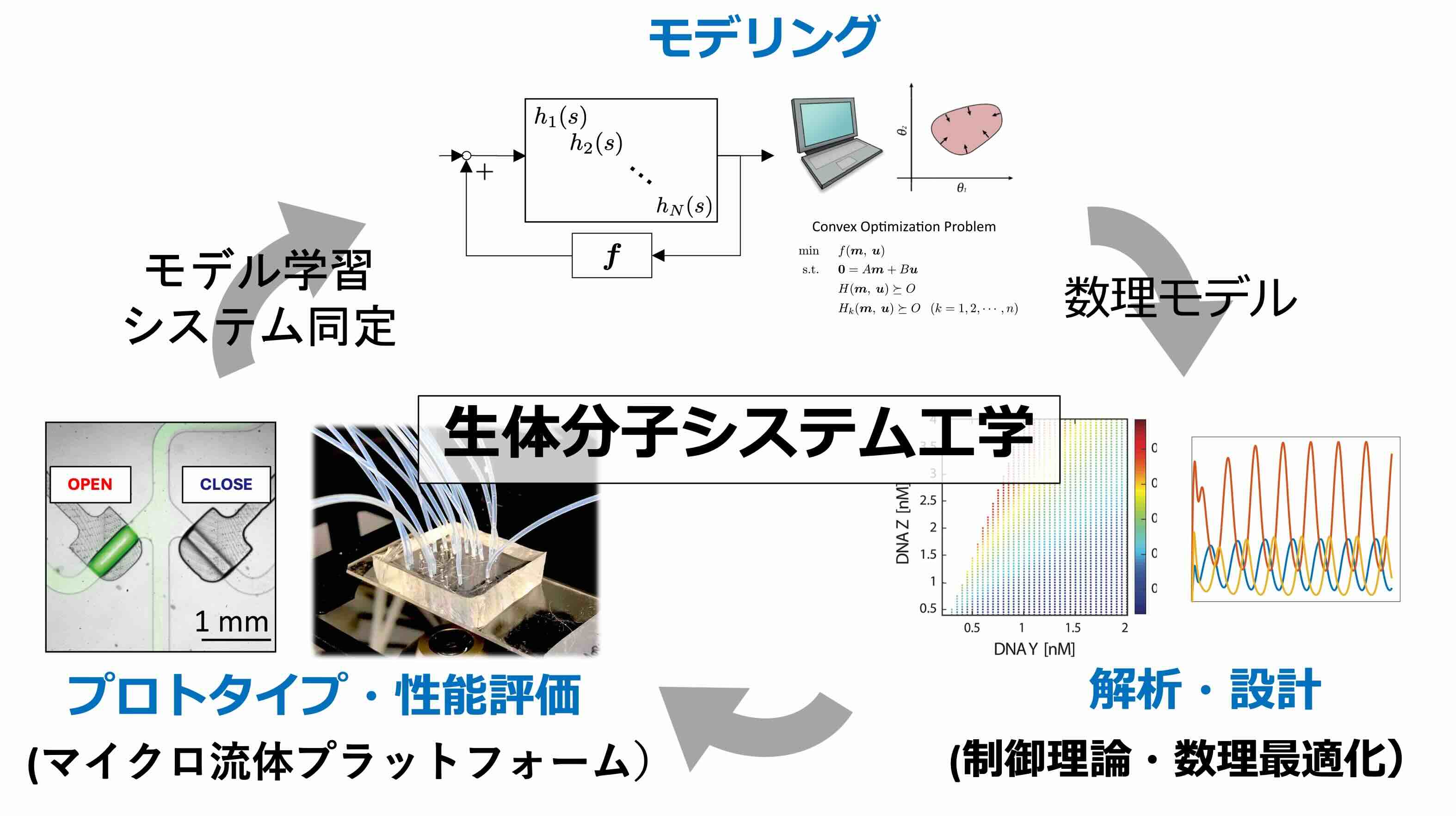
そこで，私たちの研究室では，システム制御工学（Systems and Control）を基盤として，微生物やDNAなどの生体分子を材料とするシステムの設計プロセスを体系化する生体分子システム工学（Biomolecular Systems Engineering）の確立を目指して研究を行っています（右図）．特に「電気回路や機械システムのように，生体分子を基盤とする反応システムを系統的に設計し制御するにはどのような理論体系と実験基盤が必要か」という問いに対して，理論と実験の両面から取り組んでいます． 分子や反応ネットワークの設計によって機能を実現する従来の合成生物学や分子ロボティクスのアプローチに加え，私たちの研究室では，分子システムにコンピュータを介したフィードバック制御を組み込み，分子システムの挙動をリアルタイム制御を通して最適化するアプローチを開拓しています． このような枠組みをサイバー生体分子システム（Cyber-Biomolecular Systems）と位置づけ，反応への人工的な介入（制御）によって，分子システムの性能やロバスト性をリアルタイムで評価し，設計や最適化の効率化・高度化を目指します．

生体分子システムのシステム制御理論

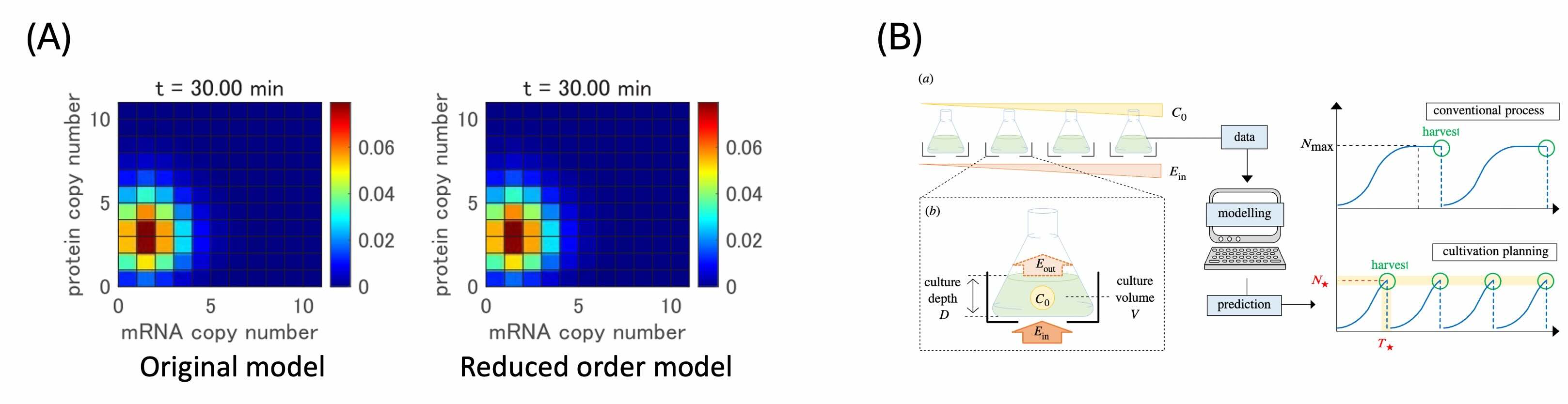
理論研究では，分子システムのダイナミクスを数理モデルとして記述し，制御理論や数理最適化の手法を用いて解析・制御するためのフレームワークを構築しています． 確率的な細胞応答のゆらぎの解析と制御 (下図(A); [IEEE L-CSS2025], [ASCC2024],[Automatica2022], [RSocInt2018])，細胞間通信に基づく分子通信ネットワークの動作解析([IEEE TNanobiosci2024], [IEEE TMBMC2023], [IEEE TMBMC2022]), 反応ネットワーク設計による所望のダイナミクス（振動子やパルス回路など）の実現 ([Automatica2022], [Automatica2013]) など，分子レベルからシステムレベルにわたる多様な問題に取り組んでいます． また，企業との共同研究では，これらの知見を応用して藻類の物質生産プロセスの最適化のような実システムの効率化にも取り組んでいます (図B; [RSocInt2022])． 最近では，機械学習と制御理論を融合した新たなアプローチにより，物理モデルの可解釈性とデータドリブン手法の柔軟性を組み合わせた，よりロバストで汎用的な解析・設計アプローチの探究も進めています．

生体分子システムの設計・構築と実験テストベッド

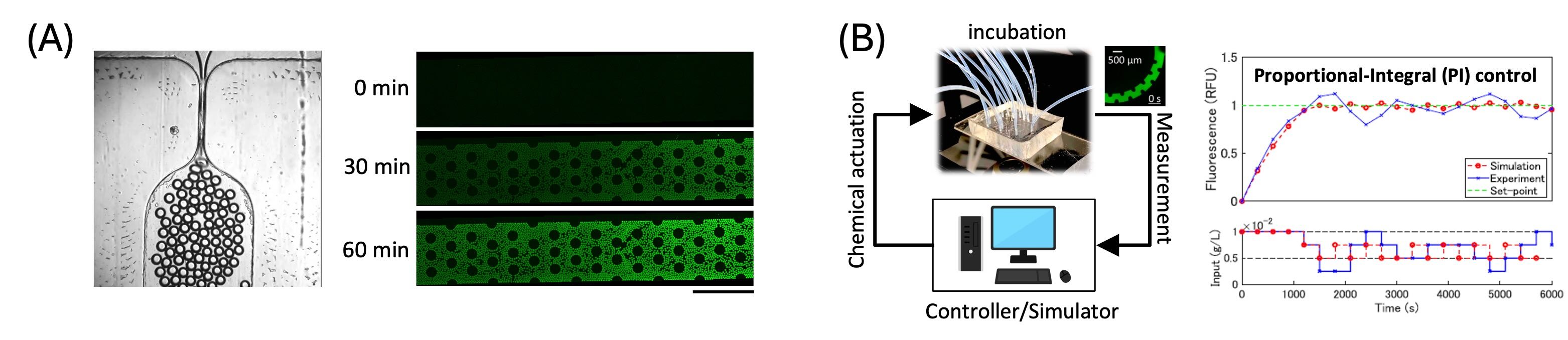
実験研究では，システム制御理論に基づく人工遺伝子回路やDNA回路の構築・設計の研究に加え，その設計プロセス自体を高速化・高度化するための自動化実験基盤の開発にも取り組んでいます ([bioRxiv2025], [RSocOpenSci2023], [SICE2022], [LoC2017], , [MolSystBiol2016], [eLife2015]など)． マイクロ流体デバイスを中心としたオートメーション技術を構築し，遺伝子組み換えやDNAナノテクノロジーによって作製した人工生体分子システムとコンピュータを閉ループで接続することで，理論と実験を相互に結ぶフィードバック型分子実験プラットフォームを実現しています． 理論と実験の往還を通じて，生体分子システムの動作を「創って操る」ための新しい設計基盤の確立を目指しています．

制御理論 × 機械学習

近年の計算機能力の飛躍的な向上と機械学習技術の発展により，データに基づいて動的システムを解析・制御する手法が急速に進展しています． このような技術的発展を踏まえ，従来のモデルベース制御理論とデータドリブンな機械学習を融合することで，複雑で変動する環境にも柔軟に適応しうる新しい制御パラダイムが形成されつつあります．

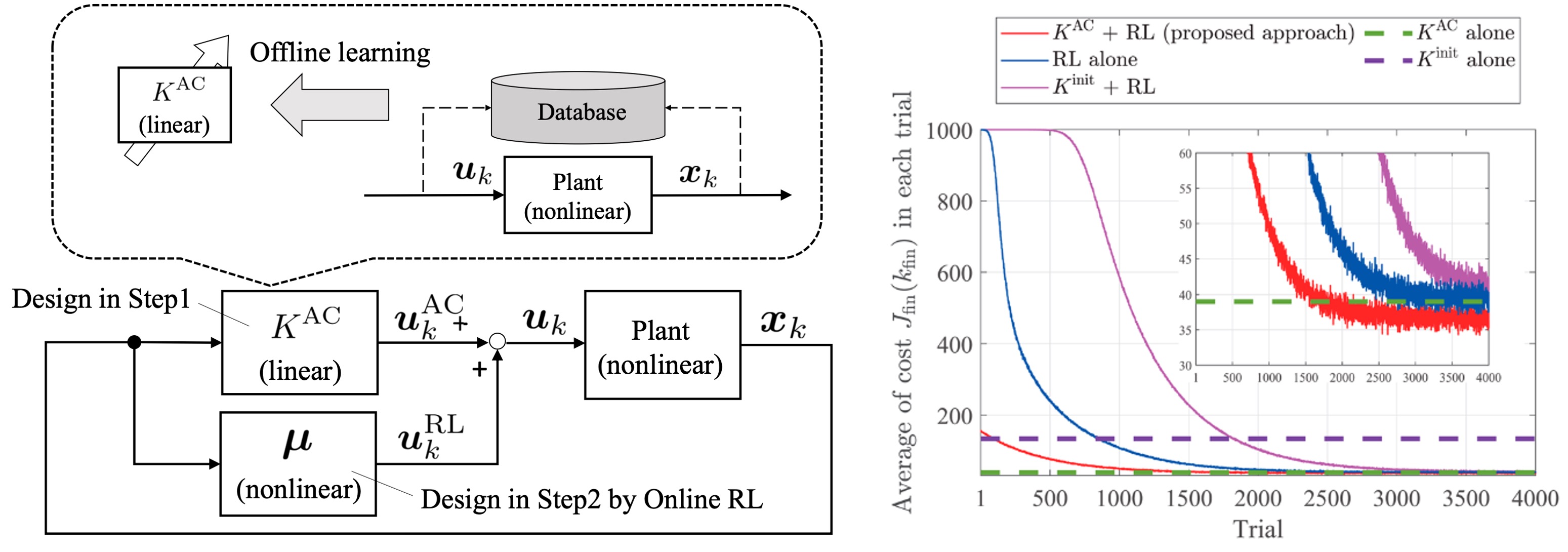
私たちの研究室では，モデルベース制御理論が持つ数理的な厳密さと可解釈性を活かしつつ，機械学習の柔軟な表現力と適応性を統合した新しい制御理論の構築を目指して研究を進めています． 特に，機械学習にドメイン知識や物理モデルを組み合わせることで，制御系の安全で効率的な学習や，閉ループ系のロバスト性を保証するための理論的基盤の確立を目指しています． 最近では，制御理論と強化学習の融合による効率的な最適制御設計手法の開発[JCMSI2023]，制御系の安全性・ロバスト性を理論的に保証する基礎理論の構築 [IEEE L-CSS2024]，さらには機械学習における数理最適化を制御理論的な視点から再構成し，計算の効率化・高速化を図るための理論研究などに取り組んでいます．